Ancient Mathematics: Fractions in Egypt
- Nicole Naporano
- Sep 1, 2021
- 6 min read
Be sure to check out the previous post in our Ancient Mathematics series: Triangles in Egypt.
Now that we know ancient civilizations were abundant with knowledge and mathematics similar to what we study today, let’s dive deeper into some of the wisdom of ancient Egypt! Remember that people from ancient civilizations had a lot of the same problems we have now--they needed to measure land, divide resources, build sturdy structures, and track the changing seasons and weather. These practical matters are what inspired the first, ancient mathematicians to create their own number systems and arithmetic.
Last time, we learned about the ways ancient Egyptians used Pythagorean triples to measure out right angles when constructing buildings and temples. The ratios used in their knotted rope tools contained whole numbers, and historians haven’t found any evidence that they had explicit knowledge of irrational numbers. This suggests that Egyptian mathematicians observed ratios in triangles by intuitive observation rather than exact calculation.
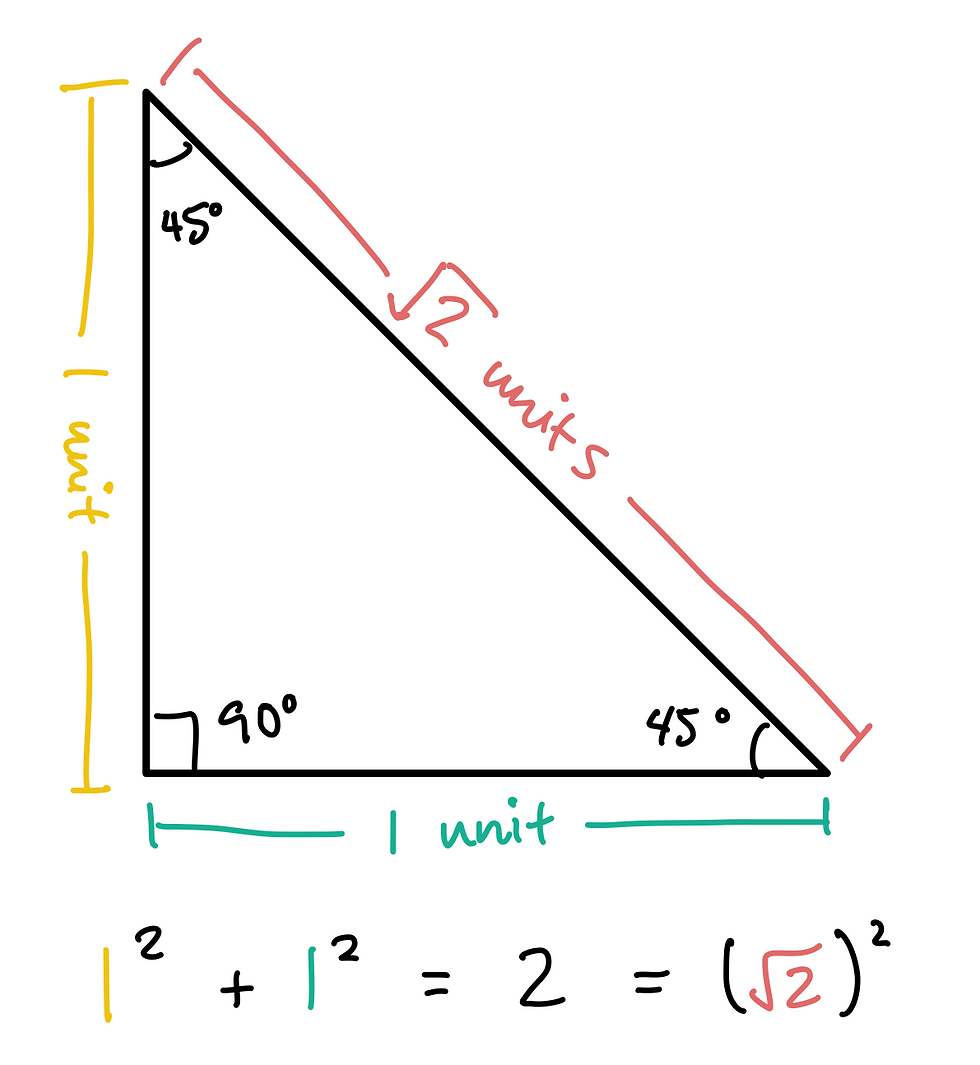
There are countless examples of Pythagorean triples containing irrational numbers--for example, the 45°-45°-90° right triangle has a hypotenuse of √2, which is an irrational number. So the fact that ancient Egyptians stuck to triangles containing whole number measurements is a fascinating example of the ways they made use of what was available to them--namely, ratios they could compute by hand!
Window to the Past
From the many artifacts and documents left behind, it is clear that the ancient Egyptians had some knowledge of the significance of ratios and rational numbers. (Recall that a rational number is a number that can be written as a single fraction, like 2/5 or 1/4.) From a historical document called the Rhind Mathematical Papyrus, we are able to get an in-depth look at how ancient mathematicians worked through some of their first written problems.

The Rhind Mathematical Papyrus was written by a scribe named Ahmes around 1550 B.C.E. in the region we now call Thebes, located near the Nile River. The document is over 16 feet long and is written in a kind of Egyptian cursive called hieratic script. If you ever find yourself at the British Museum in London, be sure to take a peek at this awesome artifact! There are lots of different sections of the papyrus to be explored--for now, we’ll take a look at the ways these ancient mathematicians expressed fractions.
There is a reference table in the Rhind Papyrus that lists a type of fraction historians call Egyptian fractions. The table consist of a series of fractions of the form
where n is replaced with odd integers between 5 and 101. Egyptians understood rational numbers to have denominators that are multiples of whole numbers (n = p*q, with p and q whole numbers) and are countable by hand, meaning that you could count all of the numbers in the table yourself if you wanted to.
There was a specific way Egyptians had of expressing a rational number
with integers p and q. The rational number would be broken up into unit fractions added together. (A unit fraction is any fraction with a numerator of 1). The following formula is recorded in the Rhind Papyrus:
For example, this formula can be used to rewrite the rational number 2/21 with p=3 and q=7:
We then get the result:
This might seem like a strange way of rewriting fractions, but we have to remember that ancient mathematicians didn’t have calculators to quickly compute numbers! When doing arithmetic by hand, it’s easier to think about fractions that all have the same numerator of 1 than it is to keep track of lots of different looking fractions.
A rational number can be expressed as this kind of Egyptian fraction as long as there are unique unit fractions that add up to the rational number. Historians aren’t sure why Egyptians didn’t want any repeated terms in their calculations. Some people think it might have something to do with a spiritual metaphor, where a numerator of 1 represents a supreme god who watches over all actions. In ancient cultures, it was common for science and religion to have intertwined meanings.
Unbelievable Precision
As far as historians can tell, there was no explicit definition for numbers which did not meet the criteria of Egyptian fractions...numbers that don't meet those criteria are what we now call irrational! Without a definition of irrational, we can conclude that ancient Egyptian mathematicians had a limited intuition of number theory--this makes it even more impressive that they achieved such remarkable precision in their calculations and constructions. The Egyptians' brute-force methods of arithmetic still led them to uncover universal constants, and there is even reason to believe Egyptians purposefully made use of the special properties of the numbers e and pi, as well as the golden ratio.
What is a universal constant?
A universal constant is a number that frequently appears in physical or mathematical formulas. Some examples are the numbers e, π, and ϕ (the golden ratio). The number mathematically denoted “e” is called Euler’s number (pronounced like “oil-er”). The number e is equal to approximately 2.718, although the decimals actually go on forever! The number pi, written π, describes the ratio between any circle’s circumference and its diameter. Pi is equal to approximately 3.14, and just like e, its decimals are infinite. The “golden ratio,” written ϕ or φ ("phi", pronounced like "f-eye" or "fee"), is equal to approximately 1.618, and it too has infinite decimals. The golden ratio appears all throughout nature--to learn more about its properties, check out this article.

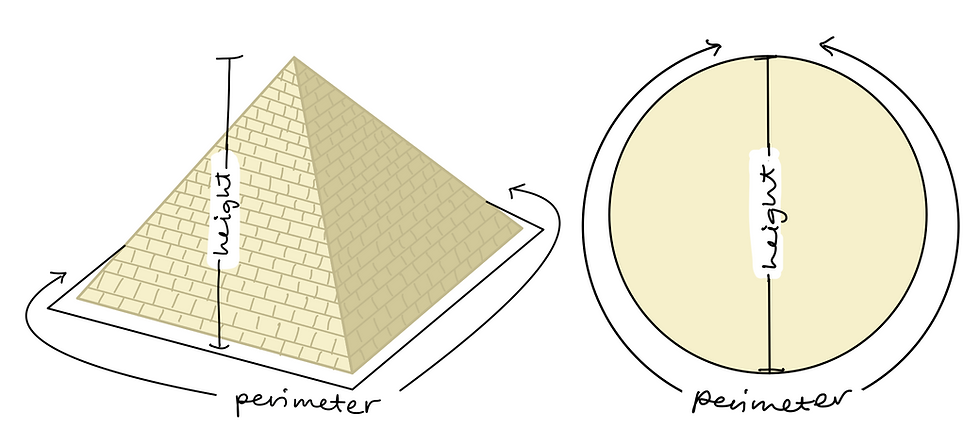
Even though ancient mathematicians may not have realized the properties of irrational numbers, they clearly had a mastery of ratios and proportions. One astonishing example of this mastery is the precision of the Great Pyramid of Giza. The relationship between the height and the base perimeter is equivalent to the relationship between a circle’s radius and its circumference, which we now know to be centered around the value pi. This means that if the pyramid’s height were the diameter of a circle, the base perimeter would be equal to the circumference.
The slope angle of the pyramid was measured from a loose casing stone to be 51.85° degrees. If you take the ratio of the angles of the pyramid’s sides and multiply it by four, you end up with the universal constant Euler’s number e, to 99.9998% accuracy!
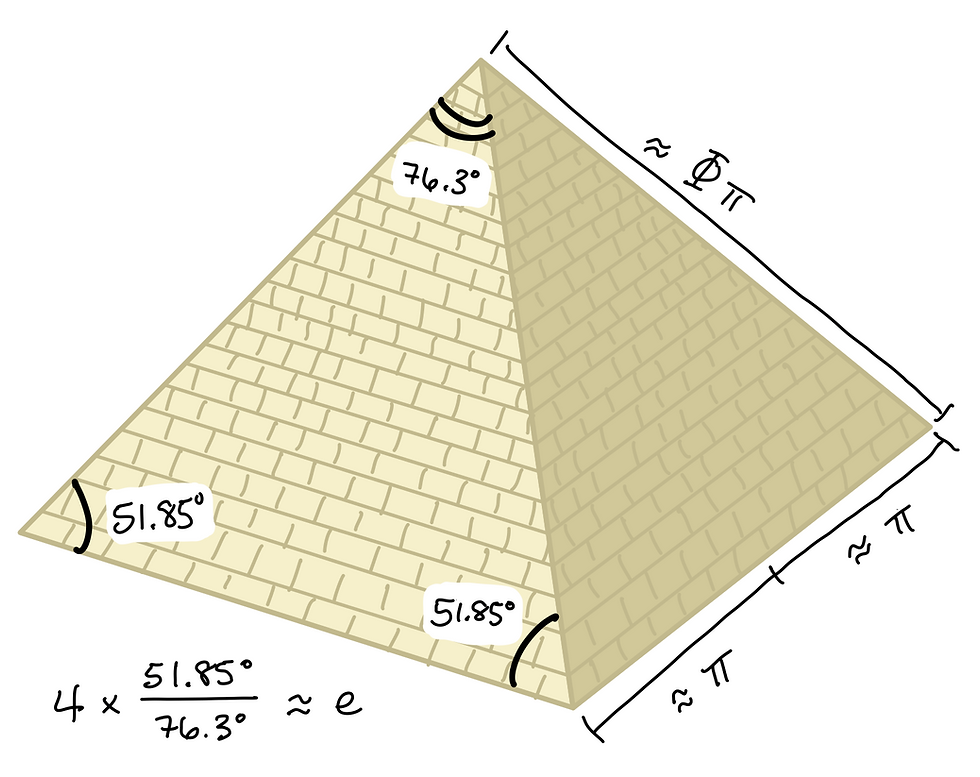
If you take the length of the pyramid’s base and divide it in half, you end up with the number pi to 99.99% accuracy! And if you take the hypotenuse of the triangles in the pyramid, you end up with the number pi multiplied by the golden ratio to 99.95% accuracy!
When you consider the fact that the pyramid could have been built with any random measurements, it’s pretty wild that they are almost exactly the values of these numbers which are foundational to our understanding of the universe.
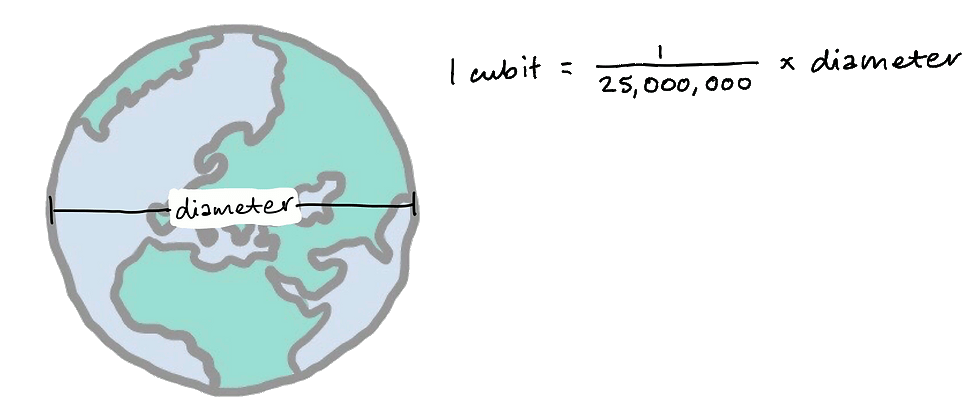
The amazing precision doesn’t end there. The unit of measure used by ancient Egyptians is called the cubit. One cubit is equivalent to 1.86 feet. This may seem like a random number in modern context, but one cubit is exactly a 1/25,000,000 ratio of the Earth’s diameter.
The height of the pyramid multiplied by 43,200 is exactly the polar radius of the Earth. The perimeter of the pyramid’s base multiplied by 43,200 is exactly the circumference of the Earth’s equator. It would be ordinary if these measurements were the result of multiplication by some ultra-precise decimal number, like 40,297.4679. But the fact that it’s a whole number ratio is what still leaves historians baffled!
The base length from corner to corner has a length of 365.242 cubits-- the exact length of one year at the time of construction was 365.242 days! If the top point of the pyramid were expressed as a coordinate, it would be 29.9792458°N, which remarkably resembles the speed of light expressed in meters per second: 299,792,458 m/s.
A Baffling Legacy
It remains one of the greatest historical mysteries whether the Egyptians knew that their marvelous structure encoded some of the most important constants of the world and the universe. A popular discussion topic is how the Egyptians might have been able to achieve a seemingly zoomed-out, other-worldly perspective by recognizing ratios of the Earth as a whole. How do you think they achieved this?!
Hopefully, it’s clear to you now that ancient civilizations were abundant with incredible wisdom, knowledge, skill, craftsmanship, and many more amazing qualities that are still a fundamental part of modern human life! In the future, we’ll explore more cultures around the world and see how ancient mathematicians paved the way for students like you and I to learn the math we use today. Remember that every time you practice trigonometry, use fractions while baking, or align your bookshelf with perfect right angles, you are taking part in a long legacy of practical mathematics.
Images courtesy of Wikimedia Commons
Written by Nicole Naporano
Edited by Madelyn Leembruggen
Explore rational numbers and the universal constants with these activities!
Interact (20-40 minutes): Measure some things around your house or classroom. See if you can find any interesting ratios within those measurements!
Define (10-20 minutes): Google search "universal constant" then try writing your own definition of this term.
Expand (15-30 minutes): Try converting any fraction to an Egyptian fraction by choosing different integers p and q!
Investigate (45-60 minutes): Learn more about e, pi, and phi. Start with the sources below, then try to find more sources on your own.








Comments